第二種電気工事士過去問
令和7年度下期
問6 (一般問題問6)

問題文

図のような三相3線式回路について、図中の✕印の箇所で断線した場合、負荷の全消費電力［kW］は。
ただし、負荷の抵抗は、30Ωとし、配線の抵抗は無視し、電源電圧は一定とする。問題文の画像

付箋

付箋は自分だけが見れます（非公開です）。

このページは閲覧用ページです。
履歴を残すには、「新しく出題する（ここをクリック）」をご利用ください。

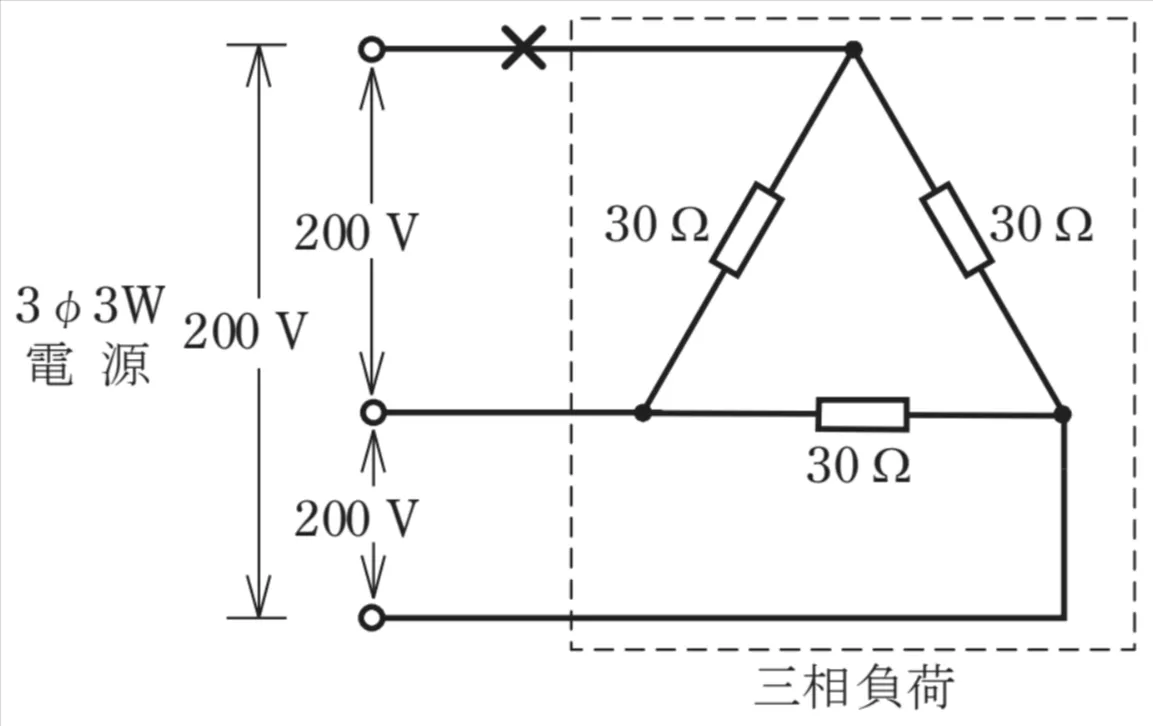
問題

第二種電気工事士試験令和7年度下期問6（一般問題問6）（訂正依頼・報告はこちら）

図のような三相3線式回路について、図中の✕印の箇所で断線した場合、負荷の全消費電力［kW］は。
ただし、負荷の抵抗は、30Ωとし、配線の抵抗は無視し、電源電圧は一定とする。

正解！素晴らしいです

残念...

断線した三相3線式回路に関する問題です。

一見難しそうに感じますが、断線すると残っている回路同士で並列回路になる点を理解出来ればすぐに解ける問題となります。

選択肢4. 2

断線すると30Ωが二つ並んでいる回路（足して60Ω）と30Ωとの並列回路となります。

この回路の合成抵抗を求めると

（60×30）÷（60+30）＝20Ωとなります。

次に電流値はオームの法則よりＩ＝Ｖ/Ｒなので

200÷20＝10Ａとなります。

最後に電力の公式はＰ＝ＶＩなので

200×10＝2,000Ｗとなり、問題ではｋＷを求めるようされているので

2,000÷1,000＝2ｋＷとなります。

まとめ

見方を変えると簡単な回路となるので、まずはしっかり問題の意味を理解して解きましょう。

参考になった数12

この問題は3相の欠相運転の問題になります。

断線した状態の回路を再度構成すると

電源が200Vで「30Ω」と「30Ωと30Ωの直列回路」が並列に繋がった回路になります。

　　　　　　　----------30Ω---------

200V

-----30Ω----30Ω-----

直列部分の抵抗を合成すると60Ωになり、次に30Ωと60Ωの並列抵抗の合成抵抗Roを算出します。

Ro＝（30×60）/（30＋60）＝1800 / 90 ＝20Ω

回路に流れる電流は、200÷20＝10Aになります。

負荷の全消費電力は10A☓200V＝2000［W］＝2[kw]

したがって、答えは2kwとなります。

参考になった数0