第二種電気工事士 過去問
令和7年度下期
問5 (一般問題 問5)
問題文
図のような三相負荷に三相交流電圧を加えたとき、各線に20Aの電流が流れた。線間電圧E［V］は。 
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
第二種電気工事士試験 令和7年度下期 問5（一般問題 問5） （訂正依頼・報告はこちら）
図のような三相負荷に三相交流電圧を加えたとき、各線に20Aの電流が流れた。線間電圧E［V］は。
- 120
- 173
- 208
- 240
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
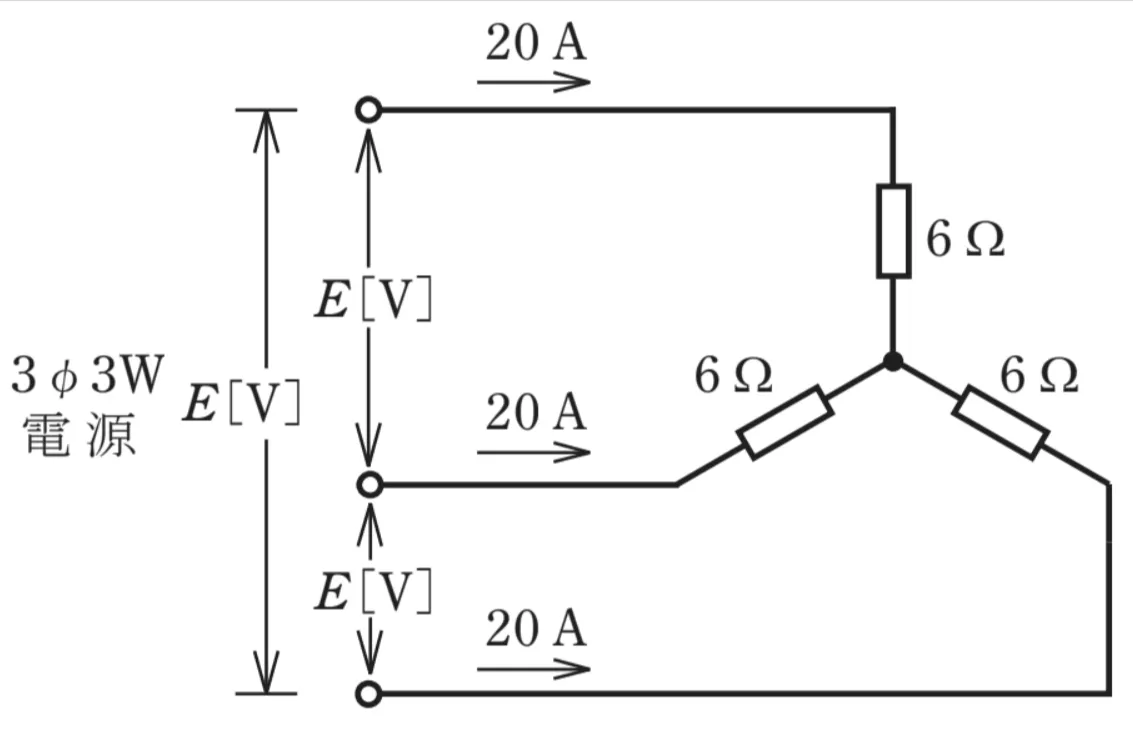
スター結線に関する問題です。
スター結線では、
・線間電圧＝√3相電圧
・線間電流＝相電流
この2点を覚えておきましょう。
相電圧は
Ｖ＝20×6＝120Ｖとなります。
問題では線間電圧を求める事になっているので、√3を掛けて求めます。
120×√3＝約207.6Ｖとなり、こちらの値が最も近い値となります。
√3は約1.7なので1.5以上2未満と覚えておけば、しっかり計算しなくても選択肢がある程度絞れます（120の1.5倍は180、2倍は240なのでその中間）。
制限時間が限られているので計算問題に時間を取られると他の問題を解く時間を取られるため、少しでも時間を短縮する方法を考えていきましょう。
参考になった数8
この解説の修正を提案する
02
これは三相3線式（3ϕ3W）
負荷は各相 6ΩのＹ(スター) 結線
各線に20 Aの線電流
求めるのは 線間電圧 E［V］となっています。
Ｙ（スター）結線で押さえておきたい内容
【電圧】√3 ☓ 各相にかかる電圧（相電圧） ＝ E（線間電圧）
【電流】線電流IＬ ＝ 相電流Iｓ
以上のようになります。
電流の関係より6Ωの抵抗に流れる電流は線電流と同じで
20Ａになるので、オームの法則より相電圧を求めます。
20（Ａ）☓ 6（Ω）＝ 120（Ｖ）
以上の結果より、電圧（＝線間電圧 E）を求めます。
E ＝ √3 ☓ 120
E ＝ 1.73 ☓ 120
E ≒ 207.6 V
正解です。
参考になった数5
この解説の修正を提案する
前の問題（問4）へ
令和7年度下期 問題一覧
次の問題（問6）へ