第二種電気工事士 過去問
令和7年度上期
問6 (一般問題 問6)
問題文
図のような単相2線式回路において、配線の長さは100m、負荷電流は10Aで、抵抗負荷が接続されている。配線の電圧降下（Vs―Vr）を4V以内にするための電線の最小太さ（断面積）［mm2］は。
ただし、電線の抵抗は表のとおりとする。
ただし、電線の抵抗は表のとおりとする。
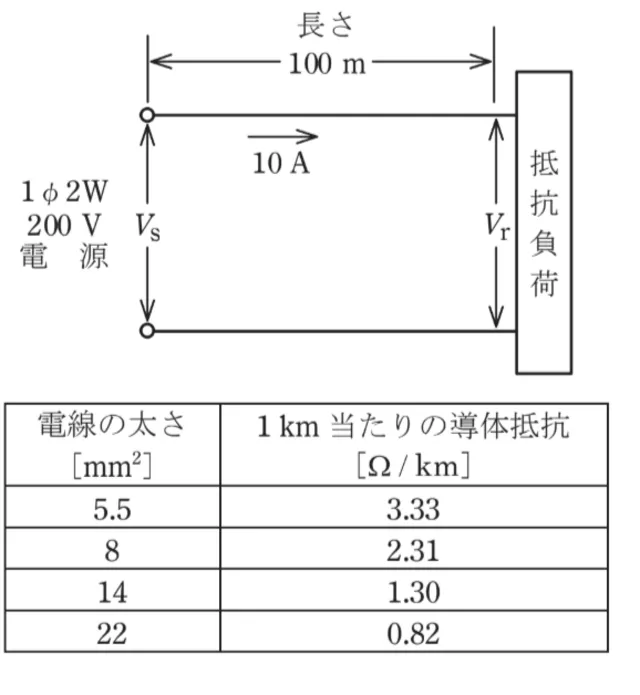
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
第二種電気工事士試験 令和7年度上期 問6（一般問題 問6） （訂正依頼・報告はこちら）
図のような単相2線式回路において、配線の長さは100m、負荷電流は10Aで、抵抗負荷が接続されている。配線の電圧降下（Vs―Vr）を4V以内にするための電線の最小太さ（断面積）［mm2］は。
ただし、電線の抵抗は表のとおりとする。
ただし、電線の抵抗は表のとおりとする。
- 5.5
- 8
- 14
- 22
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
この問題は、単相2線式回路の電圧降下の問題です。
電圧降下の式、単相２線式=2IR
配線の電圧降下4V以内にするとあるのでそれぞれ計算してみると
・5.5mm2 ２ 10×0.333=6.66 ４Ｖを超過
・8mm2 2×１０×0.231=4.62 4Vを超過
・14mm2 2×１０×0.13=2.6 4V以内
・22mm2 2×10×0.082=1.64 4V以内
条件より電圧降下を4V以内するための電線の最小太さ（断面積）［mm2］は14mm2となります。
間違いです。
間違いです。
電線の最小太さ（断面積）［mm2］は14mm2となりますので正解です。
間違いです。
公式をしっかりと頭に覚えさせましょう。
参考になった数23
この解説の修正を提案する
02
単相2線式の抵抗に関する問題です。
今までにあまり類を見ない内容ですが、しっかり文章を読んで解いていきましょう。
単相2線式の電圧降下の式は2×抵抗×電流となり、配線の電圧降下を4V以内という条件なので、
2×抵抗×10≦4Vが成り立ち、この式を整理すると抵抗≦0.2となります。
つまり、導体抵抗が0.2より小さいものが電線の最小太さ（断面積）となるので、表より電線太さ14ｍｍが適切となります。
条件を元に回路内の必要な値を求めていくので、公式が分からないと解けません。そのため、この公式に限りませんが、電気工事士の試験で出題される公式は全て覚えておく事が大事です。
参考になった数15
この解説の修正を提案する
03
配線長さは片道100mだけど、電圧降下は往復の導体抵抗で決まるから 実効長さ = 2 × 100 m = 200 m = 0.2 km と考えます。
電圧降下は V = I × R で、R = ([Ω/km]) × 0.2（km）になります。
各太さについて計算すると：
•5.5 mm²： R=3.33 Ω/km → R = 3.33×0.2=0.666 Ω→ V=10×0.666 = 6.66 V よって×
•8 mm²： R=2.31 Ω/km → R = 2.31×0.2=0.462 Ω→ V=10×0.462 = 4.62 V よって×
•14 mm²： R=1.30 Ω/km → R = 1.30×0.2=0.26 Ω→ V=10×0.26 = 2.6 V よって〇
•22 mm²： R=0.82 Ω/km → R = 0.82×0.2=0.164 Ω→ V=10×0.164 = 1.64 V よって〇
電圧降下を4V以内にするには 14 mm²と 22 mm²最小を聞いているので、14ｍｍ2になります。
参考になった数4
この解説の修正を提案する
前の問題（問5）へ
令和7年度上期 問題一覧
次の問題（問7）へ